LeetCode 218: The Skyline Problem

发表于 | | 阅读次数:
字数统计: 1.2k | 阅读时长 ≈ 5

题目链接

https://leetcode.com/problems/the-skyline-problem/

题意

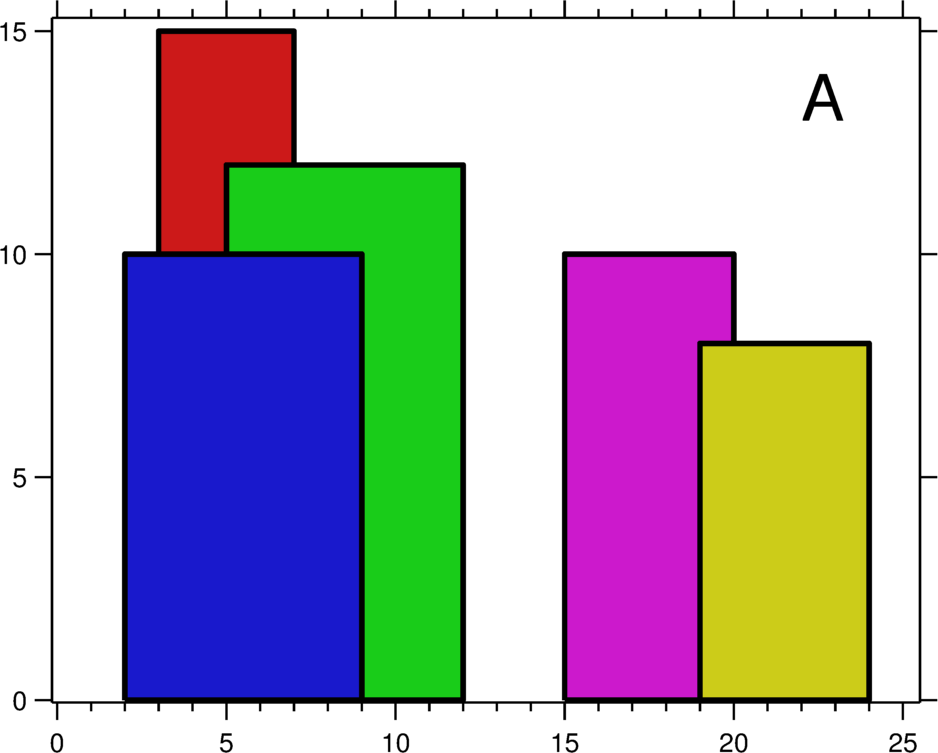
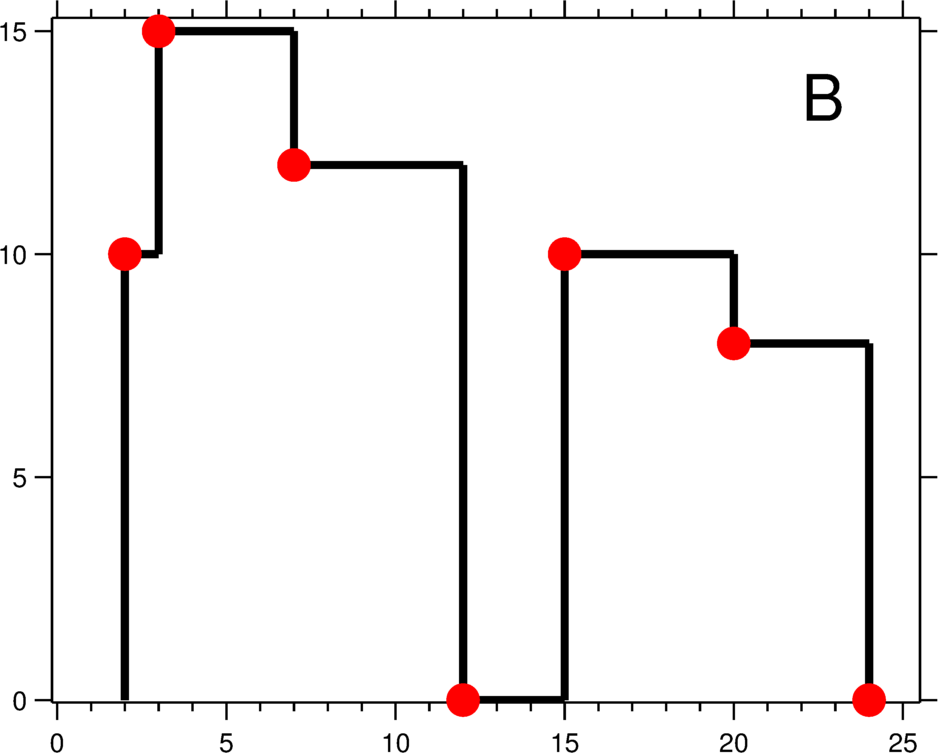
城市的天际线是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。现在，假设您获得了城市风光照片（图A）上显示的所有建筑物的位置和高度，请编写一个程序以输出由这些建筑物形成的天际线（图B）。

每个建筑物的几何信息用三元组 [Li，Ri，Hi] 表示，其中 Li 和 Ri 分别是第 i 座建筑物左右边缘的 x 坐标，Hi 是其高度。可以保证 0 ≤ Li, Ri ≤ INT_MAX, 0 < Hi ≤ INT_MAX 和 Ri - Li > 0。您可以假设所有建筑物都是在绝对平坦且高度为 0 的表面上的完美矩形。

例如，图A中所有建筑物的尺寸记录为：[ [2 9 10], [3 7 15], [5 12 12], [15 20 10], [19 24 8] ] 。

输出是以 [ [x1,y1], [x2, y2], [x3, y3], … ] 格式的“关键点”（图B中的红点）的列表，它们唯一地定义了天际线。关键点是水平线段的左端点。请注意，最右侧建筑物的最后一个关键点仅用于标记天际线的终点，并始终为零高度。此外，任何两个相邻建筑物之间的地面都应被视为天际线轮廓的一部分。

例如，图B中的天际线应该表示为：[ [2 10], [3 15], [7 12], [12 0], [15 10], [20 8], [24, 0] ]。

题目类型

几何

题目分析

看了Eason Liu 的技术博客以后才明白的。

观察样例可以发现轮廓点产生在当前的最高的矩形高度发生变化时，维护动态最高的矩形高度需要使用堆来进行。其次当矩形右端点出现时，需要将堆栈中对应的左端点移出堆，这里可以使用一个map做记录打懒标记的方式保证堆顶的最高高度仍是右端点没有出现的，堆顶懒标记不为0则一直退。

将左右端点都加入排序后，依次扫描每个端点，统计查看高度变化记录轮廓点。这里还有非常重要的一点是排序方法：

  1. x不同时按x大小排
  2. x相同，类型不同时左端点排在前面
  3. 类型相同时，左端点按高度从大往小排，右端点按高度从小往大排

提一下第3点，左端点从大往小是显然的，不然x相同时可能莫名扫出多个轮廓点，右端点从小往大是可以把小点先打标记不退出，一样是避免错误统计。具体可以推两个例子就明白了。由此可以写出源代码1。

随后可以发现代码可以简化，懒标记是由于priority_queue并没有删除功能，因此可以用mutliset直接删，排序的时候只要将左节点的高度取负就可以完全实现和上文相同的排序效果，直接用pair默认排序就完了，代码可以得到极大简化，由此得到源代码2。

时间复杂度

$O(N * log _{2} N)$

源代码1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#define LEFT 0
#define RIGHT 1
struct node {
    int x, y;
    int type;
    node(int _x, int _y, int _type): x(_x), y(_y), type(_type) {}
};
bool cmp(node a, node b) {
    if (a.x != b.x)
        return a.x < b.x;
    if (a.type == LEFT && b.type == LEFT)
        return a.y > b.y;
    if (a.type == RIGHT && b.type == RIGHT)
        return a.y < b.y;
    return a.type == LEFT;
}
class Solution {
public:
    vector<pair<int, int>> getSkyline(vector<vector<int>>& buildings) {
        vector<node>lines;
        for (auto &building : buildings) {
            lines.emplace_back(building[0], building[2], LEFT);
            lines.emplace_back(building[1], building[2], RIGHT);
        }
        sort(lines.begin(), lines.end(), cmp);
        priority_queue<int>heap;
        unordered_map<int, int>mp;
        int pre = 0, cur = 0;
        heap.push(0);
        vector<pair<int, int> >ans;
        for (auto &line: lines) {
            if (line.type == LEFT) {
                heap.push(line.y);
            } else {
                ++mp[line.y];
                while (!heap.empty() && mp[heap.top()] > 0) {
                    --mp[heap.top()];
                    heap.pop();
                }
            }
            cur = heap.top();
            if (cur != pre) {
                ans.emplace_back(line.x, cur);
                pre = cur;
            }
        }
        return ans;
    }
};

源代码2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    vector<pair<int, int>> getSkyline(vector<vector<int>>& buildings) {
        vector<pair<int, int> >lines;
        for (auto &building : buildings) {
            lines.emplace_back(building[0], -building[2]);
            lines.emplace_back(building[1], building[2]);
        }
        sort(lines.begin(), lines.end());
        multiset<int>heap;
        int pre = 0, cur = 0;
        heap.insert(0);
        vector<pair<int, int> >ans;
        for (auto &line: lines) {
            if (line.second < 0) {
                heap.insert(-line.second);
            } else {
                heap.erase(heap.find(line.second)); // 只删一个
            }
            cur = *heap.rbegin();
            if (cur != pre) {
                ans.emplace_back(line.first, cur);
                pre = cur;
            }
        }
        return ans;
    }
};
0%